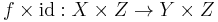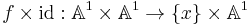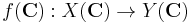Proper morphism

In algebraic geometry, a proper morphism between schemes is an analogue of a proper map between topological spaces.

1 Definition
2 Examples
3 Properties and characterizations of proper morphisms
- 3.1 Valuative criterion of properness
4 See also
5 References
6 External links

Definition

A morphism f : X → Y of algebraic varieties or schemes is called universally closed if all its fiber products

$f \times \textrm{id}: X \times Z \to Y \times Z$

are closed maps of the underlying topological spaces. A morphism f : X → Y of algebraic varieties is called proper if it is separated and universally closed. A morphism of schemes is called proper if it is separated, of finite type and universally closed ([EGA] II, 5.4.1 [1]). One also says that X is proper over Y. A variety X over a field k is complete when the constant morphism from X to a point is proper.

Examples

The projective space P^d over a field K is proper over a point (that is, Spec(K)). In the more classical language, this is the same as saying that projective space is a complete variety. Projective morphisms are proper, but not all proper morphisms are projective. Affine varieties of non-zero dimension are never proper. More generally, it can be shown that affine proper morphisms are necessarily finite. For example, it is not hard to see that the affine line A¹ is not proper. In fact the map taking A¹ to a point x is not universally closed. For example, the morphism

$f \times \textrm{id}: \mathbb{A}^1 \times \mathbb{A}^1 \to \{x\} \times \mathbb{A}^1$

is not closed since the image of the hyperbola uv = 1, which is closed in A¹ × A¹, is the affine line minus the origin and thus not closed.

Properties and characterizations of proper morphisms

In the following, let f : X → Y be a morphism of varieties or schemes.

If X, Y are varieties over the field of complex numbers C, it induces a continuous function

$f(\mathbf{C}): X(\mathbf{C}) \to Y(\mathbf{C})$

between their sets of complex points with their complex topology (see GAGA). It can be shown that f is a proper morphism if and only if f(C) is a proper continuous function.

Properness is a local property on the base, i.e. if Y is covered by some open subschemes Y_i and the restriction of f to all f^-1(Y_i) is proper, then so is f.
By definition, proper morphisms are stable under base change.
The composition of two proper morphisms is proper.
Closed immersions are proper.
More generally, finite morphisms are proper. This is a consequence of the going up theorem.
Conversely, every quasi-finite and finite presentation proper morphism is finite. This follows from the so-called Stein factorization, namely the existence of an intermediate scheme such that a morphism can be expressed as one with connected fibres, followed by a finite morphism. (EGA III, 4.3.3) This is a deep theorem.
Proper morphisms are closely related to projective morphisms: If f is proper over a noetherian base Y, then there is a morphism: g: X' →X which is an isomorphism when restricted to a suitable open dense subset: g^-1(U) ≅ U, such that f' := fg is projective. This statement is called Chow's lemma.

Proper finite presentation morphisms of schemes or complex analytic spaces preserve coherent sheaves, in the sense that the higher direct images Rⁱf_∗(F) (in particular the direct image f_∗(F)) of a coherent sheaf F are coherent (EGA III, 3.2.1). This boils down to the fact that the cohomology groups of projective space over some field k with respect to coherent sheaves are finitely generated over k, a statement which fails for non-projective varieties: consider C^∗, the punctured disc and its sheaf of holomorphic functions $\mathcal O$ . 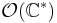Its sections $\mathcal O(\mathbb C^*)$ is the ring of Laurent polynomials, which is infinitely generated over C.
If f: X→Y and g:Y→Z are such that gf is proper and g is separated, then f is proper. This can for example be easily proven using the following criterion:

Valuative criterion of properness

There is a very intuitive criterion for properness which goes back to Chevalley. It is commonly called the valuative criterion of properness. Let f: X → Y be a morphism of finite type of noetherian schemes. Then f is proper if and only if for all discrete valuation rings R with fields of fractions K and for any K-valued point x ∈ X(K) that maps to a point f(x) that is defined over R, there is a unique lift of x to . (EGA II, 7.3.8). Noting that Spec K is the generic point of Spec R and discrete valuation rings are precisely the regular local one-dimensional rings, one may rephrase the criterion: given a regular curve on Y (corresponding to the morphism s : Spec R → Y) and given a lift of the generic point of this curve to X, f is proper if and only if there is exactly one way to complete the curve.

Similarly, f is separated if and only if in all such diagrams, there is at most one lift 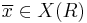$\overline{x} \in X(R)$ .

For example, the projective line is proper over a field (or even over Z) since one can always scale homogeneous co-ordinates by their least common denominator.

References

Grothendieck, Alexandre; Dieudonné, Jean (1961), "Éléments de géométrie algébrique (rédigés avec la collaboration de Jean Dieudonné) : II. Étude globale élémentaire de quelques classes de morphismes", Publications Mathématiques de l'IHÉS 8: 5–222, doi:10.1007/BF02699291, ISSN 1618-1913, http://www.numdam.org:80/numdam-bin/feuilleter?id=PMIHES_1961__8_ , section 5.3. (definition of properness), section 7.3. (valuative criterion of properness)
Grothendieck, Alexandre; Dieudonné, Jean (1966), "Éléments de géométrie algébrique (rédigés avec la collaboration de Jean Dieudonné) : IV. Étude locale des schémas et des morphismes de schémas, Troisième partie", Publications Mathématiques de l'IHÉS 28: 5–255, ISSN 1618-1913, http://www.numdam.org:80/numdam-bin/feuilleter?id=PMIHES_1966__28_ , section 15.7. (generalisations of valuative criteria to not necessarily noetherian schemes)
Hartshorne, Robin (1977), Algebraic Geometry, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90244-9, MR 0463157

External links

V.I. Danilov (2001), "Proper morphism", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=P/p075450